Feel free to check out some of my projects below!

Extreme Learning Machines vs Multiple Linear Regression in Hydrology

Wingspan or Height? Looking at What Measurables Matter in the NBA

A Unique Webapp That Allows People to Rent their Cottages

A Finite Element Analyisis Model That Solves Structural Engineering Problems

Test Your Tic Tac Toe Skills Against a Computer That Plays Optimally

Application of Extreme Learning Machines in hydrology.

View the code below to see a data project I did where an Extreme Leraning Machine (ELM) was used toe hydrology-forecast hydrological data for a river basin in Spain!

Both ELM and Multiple Linear Regression (MLR) were used to create this forecast, and the results ended up being quite similar!

When I initially developed the codes to complete the forecasts, I thought MLR was going to be much less effective than ELM. This is because ELM is a feedforward neural network with a hidden layer, and it sounds like this type of machine learning architecture would be more effective than something that can easily be done in Microsoft Excel such as MLR.

This being said, when you look at the mathematics behind ELM, it is closer to MLR than one would think.

ELM is a feedforward neural network, there's no backpropogation in the method at all. The weights and biases are randomly set, as would be done in any neural network.

However, there's a key difference here. Those weights and biases aren't trained using backpropogation. Some fun math is done which can be seen in the source code, but due to the random weights and biases, the final vector that is used to generate the output is solved analytically in a manner similar to MLR.

I also completed analysis using Support Vector Regression. This method performed slightly worse that both MLR and ELM, which makes sense based on how these methods typically perform in similar types of applications.

I'm going to take the same dataset and look to apply some other neural network architectures, particularly one that uses backpropogation to hopefully decrease the overall cost of the objective function. I'm also going to use a recurrent neural network, preferably an LSTM as these are successful when used in hydrology.

Source Code

Wingspan or Height? Looking at What Measurables Matter in the NBA

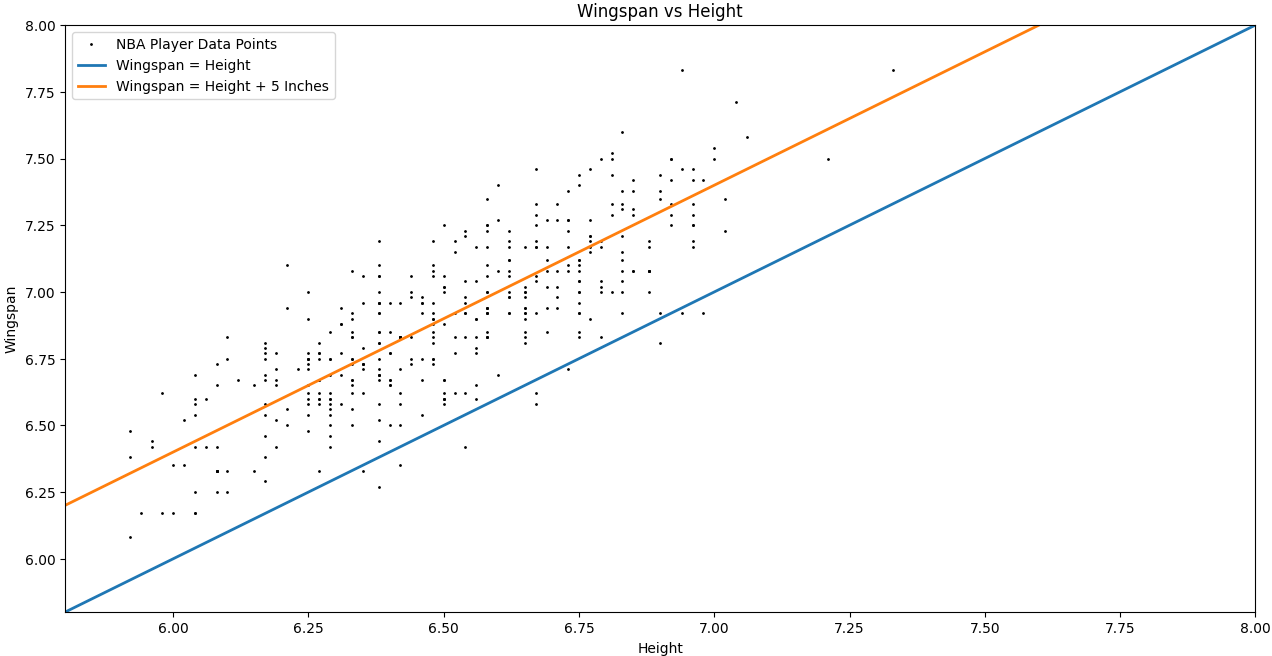
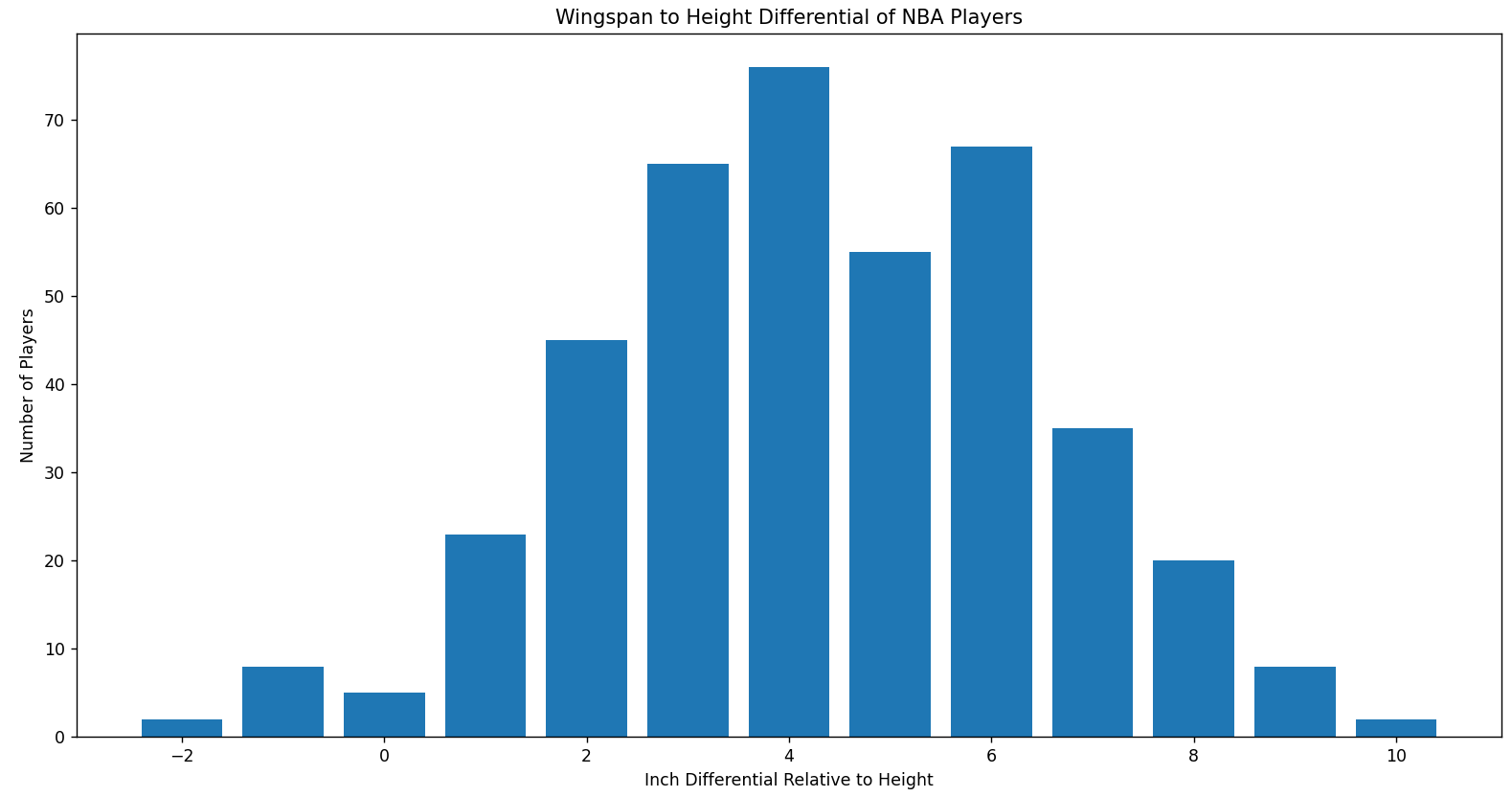
As someone who plays basketball quite often, I noticed that there is a significant advantage that comes with having a long wingspan. On the defensive end, it allows you to be much more effective by getting loose balls, and generating steals and turnovers. Many of the best defensive players in the NBA have incredibly long wingspans relative to their height, including:

1. Kawhi Leonard
2. Rudy Gobert
3. Giannis Antetokounmpo
4. Draymond Green

A lot of highly effective offensive players also have long wingspans. Kevin Durant has a 7'6" wingspan, giving him the ability to easily shoot over smaller defenders. However, the majority of the advantages of having a long wingspan come on the defensive end.

Most people have wingspans that are approximately equal to the height. I was curious to see whether this held true in the NBA. I initially assumed that it wouldn't, as it would make sense that players with longer wingspans relative to their heights would be more effective players, and then be able to make the NBA.

To test this out, I scraped the height and wingspan data of all the current NBA players off the internet using Selenium and Beautiful Soup. I then plotted all the data points using Matplotlib, along with a 1 : 1 line. I then plotted a line that is 1 : 1 + 5", which is actually a much closer representation of the NBA data. This indicates that having a longer wingspan than height is very valuable in basketball. The graph can be seen below, and the source code can be found here. There is also a bar chart that demonstrates how long NBA player wingspans are in relation to their heights.



Timesharewebapp:

As its name suggests, Timesharewebapp is a web app that allowed cottage owners to rent out their properties online. The app was created in such a way so that owners were able to rent their cottage to specific people, and therefore they did not have to worry about their cottage being rented by people who they didn't pre-approve.

The app was created with Meteor.JS, MongoDB, Stripe, Bootstrap, HTML, CSS, and Javascript.

Please view the source code at the following link: Source Code

Finite Element Analysis Problem Solver

Finite Element Analysis (FEA) is a numerical simulation method that is widely used in engineering and science to analyze complex physical systems. The method is based on the discretization of the system into smaller, finite elements, which can be easily analyzed using numerical techniques. The FEA method is used to solve problems in a wide range of fields, including structural analysis, fluid mechanics, heat transfer, and electromagnetic field analysis.

FEA works by dividing a complex system into small, interconnected elements or meshes. Each mesh is then analyzed using mathematical equations to calculate the behavior of the system. These equations are based on the physical properties of the materials used in the system and the loads applied to it. The equations are then solved using numerical techniques, such as the finite element method, to obtain a solution for the behavior of the system.

FEA has numerous applications in different fields, including aerospace, automotive, civil, and mechanical engineering. In aerospace, FEA is used to design and analyze aircraft structures, landing gear, and engine components. In automotive engineering, FEA is used to analyze the behavior of car components, such as the suspension, frame, and bodywork. In civil engineering, FEA is used to analyze the behavior of buildings, bridges, and dams. In mechanical engineering, FEA is used to analyze the behavior of machines, such as engines, turbines, and pumps. The FEA method is also used in medical science to analyze the behavior of implants and prosthetics.

I wrote a piece of code that solves traditional beam systems in structural engineering based on inputs from the user. These inputs include the loading, and the supports that the structure has within it. This allows highly indeterminate structures to be analyzed by hand. The code was written in MATLAB, and has proven to be useful in school when analyzing complex systems. Source Code

Tic Tac Toe:

Since Tic Tac Toe is a solved game, I decided to create a program that plays optimally.

The computer plays first, and cannot lose. The player can tie the computer if they play optimally. Please view the source code at the following link: Source Code